Ввод

Результат

a over b+2

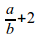
a over {b+2}

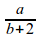
a^2+b^2=c^2

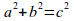
lim csub{a%tendto infinity} bar V_n

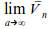
left lbrace stack{x+y=5{~} # 2y-6=x # xy=-3{~}} right none

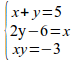
{sin 2x}over{1+sin x}=-2cos x

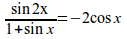
sqrt{25-4x^2}(3sin 2%pi x+8cos %pi x)=0

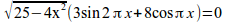
log_{3}(5x^2+6x+1) leslant 0

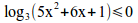
left lbrace stack{3x+ay=nroot{5}{2}# ax+3y=4{~}} right none

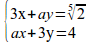
int from{-2}to{-1 over %pi}{dx over{x sqrt{x^2-1}}}

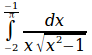
sum from{n=1}to{infinity}{left ( ctg{n%pi}over{4n-2} -sin{n%pi}over{2n+1} right )}

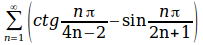
{sin 2x}over{sin 3x}=1

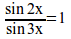
sqrt{x^3-4}=cos x

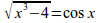
log_{sin{%pi}over{12}}(x^2x+{35}over{24})geslant 0

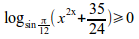
left lbrace stack{(x-a)nroot{4}{x+y}=0 # x+y-abs{x}=2{~}{~}} right none

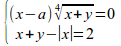
int from {0}to{2 %pi}{{dx}over{sin^4 x+cos^4 x}}

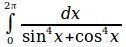
sum from{n=1}to{infinity}{{1}over{ln^2 left ( sin{1}over{n} right )}}

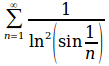
{2-3sin x -cos 2x}over{6x^2-%pi x-%pi^2}=0

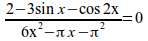
nroot{3}{x-2}+sqrt{x+1}=3

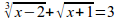
{5}over{2}log_{5}nroot{5}{x}-{1}over{3}log_{sqrt{5}}geslant 1

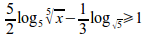
left lbrace stack{2x+3y=5 {~}# x-y=2{~}{~}} right none

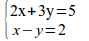
int from{{-%pi}over{3}}to{3}{arcsin sqrt{x over{1+x}}dx}

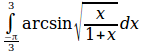
sum from{n=1}to{infinity}{sqrt{n+a}-nroot{4}{n^2+n+b}}

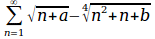
log_{{2}over{sqrt{2-sqrt{3}}}}(x^2-4x-2)=log_{{1}over{2-sqrt{3}}}(x^2-4x-3)

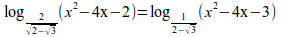
x^{3}-3x=8{1}over{8}

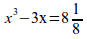
{1}over{lg x}+{nroot{3}{5-x}}over{1-lg x}leslant 1

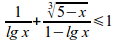
left lbrace stack{x+3ay=1{~}{~}{~}{~}# ax-3ay=2a+1} right none

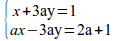
I_n = int from{0} to {%pi over 4}{left ( {sin x-cos x}over{sin x+cos x} right )^{2n+1}dx }

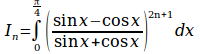
sum from{n=1}to{infinity}{1 over{sqrt{n}} - sqrt{ln{{n+1}over{n}}}}

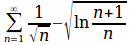
log_{x}{4x+5}over{6-5x}=-1

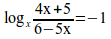
log_{x+1}(x^2+x-6)^2=4

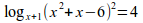
(sqrt{5}+2)^{x-1}geslant (sqrt{5}-2)^{{x-1}over{x+1}}

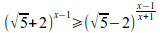
left lbrace stack{xy=4{~}{~}{~}{~}{~}{~}{~}{~}{~}{~}{~}{~}# (log_{a}x)^2={3}over{5}(log_{a}4)^2} right none

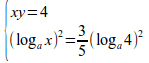
I_{n}=int from{0}to{1}{{x^n dx}over{sqrt{1-x^2}}}

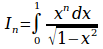
sum from{n=1}to{infinity} {left ( a^{1 over n}-{b^{1 over n}+c^{1 over n}}over 2 right )}

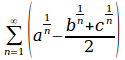
log_{x^2}{4x-5}over{abs{x-2}}={1}over{2}

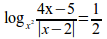
(log_{sin x}cos x)^2=1

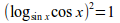
left ({1}over{4} right )^x leslant 2^{3-x}+25^{{1}over{log_{3}5}}

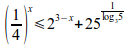
left lbrace stack{y-abs{x-a}=1 {~}{~}{~}{~}{~}# log_{a}y^3={5}over{2}nroot{3}{x-4}}right none

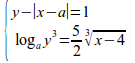
int from{0}to{1}{x^15 sqrt{1+x^8}dx}

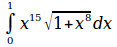
u_n=sum from{0}to{1 over %pi}{{sqrt{x}dx}over{1+x^2}}

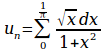
{2 sin^2 x-cos 2x}over{12x^2-4%pi x-%pi^2}=0

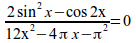
x^3+2x-5 nroot{6}{3}=0

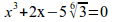
5^{x^2+x-1}geslant left ( {1}over{5} right )^{5x^2}

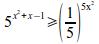
left lbrace stack{log_{y}x+log_{x}y={5}over{2}# x+y=a^2+a{~}{~}{~}} right none

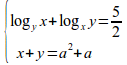
int from{0} to{%pi} {{x sin x}over{1+cos^2 x} dx}

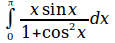
x_n=sum from{k=1}to{n}{{ln k}over k-{(ln n)^2}over{2}}

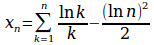
log_{3}left ( {1}over{3} -abs{{3%pi}over{2}-x} right ) =sin x

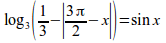
sqrt{sin 4x}+sqrt{cos 4x}=1

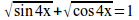
1+log_{{1}over{2}}(3x^2+2)geslant log_{2}{nroot{5}{2}}over{2x+5}

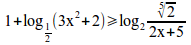
left lbrace stack{(2^{x}+1)2^{y+1}=a# sqrt{x^2+y^2}=x+y} right none

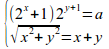
int from{e^{-2%pi n}} to{1} abs{cos x left ( ln 1 over x right ) }dx

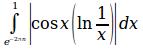
sum from{n=1}to{infinity}{(-1)^n {sqrt{n}}over{n+100}}

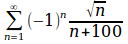
{cos 2x - sin 2x}over{12x^2-8%pi x+%pi^2}=0

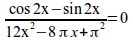
x^4-2 sqrt{2}x^2-x+2-sqrt{2}=0

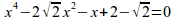
log_{{1}over{2}}{5x+4}over{x-2}geslant tg{5%pi}over{4}

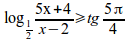
left lbrace stack{x sqrt{x^2+y^2}+ax=0{~}{~}{~}# y nroot{5}{x^2+y^2}+ay+1=0} right none

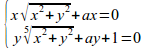
int from{1 over 2} to{2} left ( 1+x-1 over x right )e^left ( x+1 over x right )dx

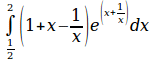
sum from{n=2}to{infinity}{(-1)^n over {sqrt{n}+(-1)^n}}